ISL: Mejora del rendimiento de los mensajes de navegación GNSS

Aprovechar los Inter-Satellite Links(ISL, enlaces entre satélites) de alta precisión para la comunicación y el alcance entre satélites GNSS ofrece una difusión de datos mejorada y más frecuente que los ODTS terrestres. 

La precisión de los mensajes de navegación de las constelaciones de satélites sigue aumentando, y la calidad mejorada de las efemérides y los relojes de los satélites beneficia directamente la precisión del posicionamiento. El siguiente gran paso hacia un mayor rendimiento aprovecha los enlaces entre satélites (ISL) [1], que permiten tanto el intercambio de datos como las mediciones de navegación (código de operador y código de fase). Las mediciones ISL, que proporcionan observabilidad intra e interplanos que “congela” la constelación, se consideran un pilar para mejorar el rendimiento de los mensajes de transmisión.

Normalmente, la precisión del servicio de navegación depende en gran medida de la confiabilidad del segmento terrestre, y la determinación de la órbita de los satélites se realiza mediante mediciones de pseudodistancia y fase de portadora recopiladas en tierra. Las efemérides de los satélites, así como las polarizaciones de los relojes a bordo, se calculan en una instalación de procesamiento terrestre y luego se cargan en cada satélite dentro del mensaje de navegación. Esto sólo puede ocurrir cuando el satélite es visible desde una instalación de enlace ascendente, lo que plantea limitaciones:

• El intervalo de actualización del mensaje de navegación se fija en el período de revisita de los satélites dada la distribución actual de estaciones terrestres de enlace ascendente, lo que supone una carga para el plan de contactos.

• El rendimiento, en términos de precisión, de la determinación de la órbita y la sincronización del reloj depende de medidas terrestres.

• Un segmento terrestre degradado (fallo de estaciones, pérdida masiva de bloqueo, rotura de red, etc.) afectaría la precisión del servicio de navegación. 

Se han propuesto ISL como solución. Un enlace de comunicación entre plataformas en órbita permite el intercambio de datos entre satélites y el alcance entre satélites (ISR). El intercambio de datos significa una difusión de datos mejorada y más frecuente y una antigüedad de los datos reducida. ISR puede servir como un observable adicional para el proceso de determinación de la órbita terrestre y sincronización de tiempo (ODTS), así como la principal entrada observable para un algoritmo de navegación autónomo a bordo, aumentando la solidez del GNSS.

Con base en los resultados de estudios previos [1-4], en este artículo apuntamos a precisiones al nivel de 10 cm al 95% en el error de señal en el espacio (SISE), incluida la órbita y el reloj transmitidos dentro del mensaje de navegación proyectado en el peor línea de visión del usuario al procesar observaciones tanto ISL como terrestres. Presentamos el nivel de rendimiento alcanzado con el Motor de Navegación para Determinación de Órbitas y Sincronización de Tiempo (NEODIS), que es el núcleo de los algoritmos de navegación desarrollados por Thales Alenia Space para la determinación precisa de la órbita de constelaciones de satélites. Estos algoritmos permiten la estimación en tiempo real de órbitas y relojes, así como la generación de mensajes de navegación con una precisión estimada en decenas de centímetros. 

Tecnología ISL

Según la Unión Internacional de Telecomunicaciones (UIT), ISL establece un enlace de comunicación por radio entre plataformas en órbita [5]. Este enlace permite la distribución de datos, telecomandos y telemetría, así como capacidades de alcance. Las antenas orientables permiten establecer un ISL ya sea en el plano o fuera del mismo. Se pueden utilizar diferentes técnicas de acceso, según los objetivos específicos de dicha comunicación y los impulsores de diseño específicos. Desde el punto de vista frecuencial, un ISL se puede establecer tanto en bandas de radiofrecuencia (RF) como en bandas ópticas. Un enlace óptico, si bien proporciona medidas más precisas, aumenta la complejidad de la plataforma. Los enlaces ópticos requieren un sistema de control de actitud más preciso, así como más potencia y un tiempo de adquisición más largo. No existe una regulación de frecuencia de la UIT para un enlace óptico. Para un enlace de RF, la selección de frecuencia debe basarse en el cumplimiento de las restricciones y regulaciones de la UIT, evitando interferencias con otros enlaces de comunicaciones, tecnología de antena y especificaciones de control de actitud, y potencia disponible.

El enlace de RF consume menos energía que el enlace óptico, tiene una velocidad de datos más débil y es menos robusto contra interferencias e interferencias de señal. Algunos diseños de sistemas consideran el uso de ISL ópticos y de RF para comunicaciones de alcance y de bajo ancho de banda [6]. La señal transmitida se puede utilizar como fuente de observables para alimentar los algoritmos ODTS (ya sea a bordo para navegación autónoma o en tierra). Se puede modular un código PRN en la portadora y luego usarlo desde el satélite receptor para calcular la hora de llegada, proporcionando una medición de pseudodistancia. Las mediciones de fase portadora se pueden realizar utilizando un bucle bloqueado de frecuencia (FLL). En algunas referencias, las medidas de pseudorango realizadas en un ISL se denominan rangos de enlace cruzado.

Las principales ventajas de ISR: 

1.  Una geometría de medidas más favorable permite una mejor observabilidad de los componentes transversales y a lo largo de la trayectoria.

2.  Casi ausencia de retrasos inducidos por la atmósfera (lo que limita la distancia mínima de la línea de visión de satélite a satélite con respecto a la superficie de la Tierra).

3.  Se pueden calcular alcances duales unidireccionales si las medidas se comparten entre parejas de satélites. 

4.  Mediciones de alta calidad debido a la alta relación portadora sobre ruido 
C/N ₀ .

Plan de contacto ISL

La arquitectura ISL define con qué frecuencia se pueden adquirir medidas y en qué época, así como la posibilidad de realizar comunicación full-duplex o half-duplex. Existen diferentes formas de diseñar el cross-link, diferentes esquemas de comunicación y la posibilidad de instalar múltiples interfaces ISL por satélite.

Algunos prevén la implementación de múltiples antenas EHF para establecer ISL. Esto mejora la solidez del sistema en capacidades de difusión, monitoreo y control y operatividad para servicios que toleran la latencia ISL. También mejora el rendimiento de ODTS.

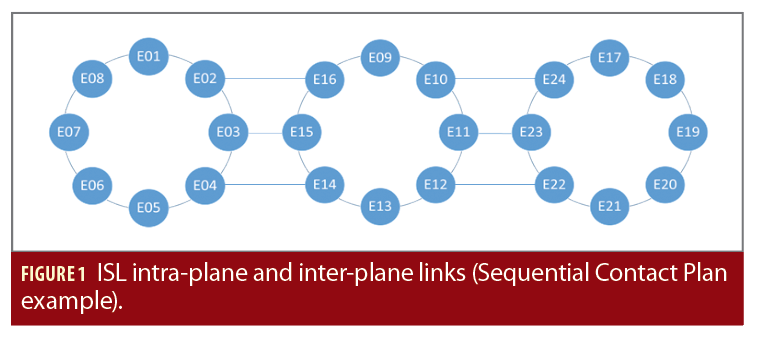
Los planes de contacto ISL previstos para este experimento son del tipo punto a punto (“unicast”) y “secuenciales”, permitiendo la comunicación entre pares de satélites, en modo semidúplex, ya sea intraplano o interplano (respectivamente, entre satélites en el mismo plano orbital y en diferentes planos orbitales) durante ciclos repetitivos. En un Plan de Contacto Secuencial, un satélite determinado intenta establecer comunicación ISL con todos los satélites uno tras otro. Esto se hace siguiendo una matriz fija, independientemente de la distancia u otros parámetros que puedan afectar al propio enlace. 

Para optimizar el rendimiento de los mensajes de navegación, se debe establecer el ISL en todos los planos para construir una red donde todos los satélites estén conectados directa o indirectamente  (Figura 1).

Para una definición exhaustiva del plan de contactos se debe definir la franja horaria, el retardo de apuntamiento y el ciclo de comunicación:

Intervalo de tiempo:  La duración de un intervalo de comunicación entre dos satélites, que incluye dos subintervalos de igual duración. Durante el primer subintervalo, el Satélite A transmite al Satélite B y viceversa durante el segundo subintervalo. La señal transmitida es utilizada por el satélite receptor para realizar mediciones y recibir datos.

Retraso de apuntamiento:  El retraso entre un intervalo de tiempo y el siguiente, necesario para apuntar la antena hacia el siguiente satélite. También incluye otros retrasos adicionales debido a los mensajes de acuse de recibo necesarios para iniciar la transmisión.

Ciclo de comunicación:  El tiempo necesario para comunicarse con todos los satélites de la constelación. Al final de un único ciclo de comunicación, todas las parejas posibles de satélites han establecido un ISL e intercambian datos/distancias.

Rango unidireccional ISL

ISL se puede utilizar para realizar mediciones de distancia convencionales entre satélites. La medida utilizada es una medida del tiempo de propagación calculada por correlación sobre un código pseudoaleatorio modulado y enviado por un transmisor. El satélite conoce la posición de cada transmisor en el sistema de coordenadas terrestres. La señal se envía de forma continua y el satélite puede realizar sus mediciones utilizando modulación CDMA en la señal recibida. Desde el momento en que el transmisor está en 
visibilidad, cada ∆t _medido  en la escala de tiempo específica del satélite, se realiza una nueva medición.

Considerando todos los efectos conocidos, el modelo para esta medición de código portador entre el centro de masas de las antenas del emisor E y del receptor R es:

• La hora  (t _r ,t _e )  expresada en la referencia horaria del sistema GNSS (STR) y la hora propia aparente en el emisor  ^{te E} y _el receptor  t _r ^R  están vinculadas por la siguiente relación:

• δ t  es el sesgo aparente del reloj del satélite (que contiene el sesgo del hardware) con respecto a STR, que puede aproximarse mediante un polinomio cuadrático 

•  D _RE  es la distancia geométrica entre el centro de masa (COM) del emisor y del receptor igual a 

siendo   y   son la posición del receptor y emisor COM respectivamente, siendo τ _RE  el tiempo de transición, τ _RE = c(t _r -t _e );

• ∆ t ^rel  es el efecto relativista excéntrico que afecta tanto a los satélites receptores como a los emisores.

con   y   la velocidad del receptor y emisor COM respectivamente;

•   es el efecto Shapiro, siendo el efecto sobre la propagación de la señal debido al campo gravitacional de la Tierra; 

Donde μ _Tierra = GM _Tierra, r _R  es la distancia del satélite R desde el centro del campo de gravedad,  r _E  la distancia del satélite E y r ₀  la distancia de la línea de visión del satélite R al satélite E desde el centro de la Tierra campo de gravedad.

•  B _R  y  B _E  son los retrasos instrumentales (en metros) relativos a la antena ISL en la cadena de recepción para R y la cadena de transmisión para E.

•  PCO  es el desplazamiento del centro de fase relacionado con los satélites emisores y receptores. Representa la distancia entre el centro de masa del satélite y la fuente aparente de radiación (centro de fase) en la antena ISL. Es diferente de las antenas de banda L utilizadas para transmitir la señal en el espacio y se supone que es una función de la orientación ISL.

• ε _M  es el ruido de medición.

Debido a que las mediciones ISR se rechazan cuando el enlace geométrico está a menos de 1.000 kilómetros de la Tierra, no hay efecto ionosférico, por lo que el modelo no tiene en cuenta el retraso de la ionosfera.

El ruido de medición se modela como un error gaussiano y depende principalmente de la longitud de un chip PRN. En general, el error es aproximadamente igual al 1% de esta longitud. Se puede calcular como: 

f _CH  es la frecuencia de modulación PRN ( f _CH = 10,23 MHz clásicamente). Sin embargo, está relacionado principalmente con el rendimiento del bucle bloqueado de retardo (DLL).

Las formulaciones anteriores de las ecuaciones de medición no muestran explícitamente las velocidades de los satélites. Eso sólo proviene de la matriz de transición de estados, que puede resultar insuficiente para su estimación. El problema es aún más evidente si consideramos la baja observabilidad de la velocidad durante la duración limitada de los arcos de medición. Por estas razones, las mediciones de alcance unidireccional se combinarán con mediciones Doppler convencionales que proporcionan información específica sobre la velocidad del satélite y mejoran su observabilidad. El modelo para esta medición deriva directamente de la definición del efecto Doppler:

La variación de la frecuencia de recepción  f _r  con respecto a la frecuencia de transmisión  f ^e  es proporcional a la velocidad radial relativa entre los dos satélites.

¿Dónde   está el vector unitario de la línea de visión que se calcula en la época  t _r  de la medición? 

Más específicamente, para una señal transmitida en la frecuencia  f ^E ,  es cierto para la frecuencia recibida  f _R

¿Dónde   está la tasa de pseudorango, la derivada temporal de  la Ecuación 1  y ∆ f = f _R – f ^E  es la salida del PLL?  La ecuación 12 es el vínculo entre el desplazamiento Doppler observable y el estado del satélite y el reloj: 

Despreciando la variación temporal de los retrasos instrumentales, el PCO y suponiendo que la derivada temporal del efecto Shapiro es pequeña en comparación con la medida y el ruido mismos, el primer término de  la Ecuación 13  se puede expresar como:

Donde el  r  apex significa que es la proyección de la velocidad en la línea de visión entre los dos satélites. La inclusión de esta medida introduce dos variables de estimación adicionales 
( ) y ( ), incluso si es posible utilizar la deriva del reloj del satélite transmisor contenida en el mensaje de navegación para el cálculo del modelado de mediciones.

El tiempo de propagación se calcula de forma iterativa a partir de las posiciones de los satélites en el momento de la medición.

Rango ISL dual unidireccional 

ISL aumenta la robustez de la constelación GNSS ante la pérdida temporal de contacto con el segmento terrestre. En este escenario degradado, el segmento espacial aún podría depender de observaciones basadas en ISL para realizar su propia OD y mantener la generación y provisión de un mensaje de navegación. Estas mediciones son la combinación de una parte dependiente de la órbita y una parte dependiente del reloj, que incluye polarizaciones de reloj tanto del receptor como del transmisor. Las observaciones ISL se recopilan una a la vez en épocas específicas. La solución más utilizada para la navegación autónoma [2, 8] separa el problema de determinación de la órbita del problema de sincronización del reloj. Esto es posible gracias a la construcción de una medición de distancia unidireccional dual en la época  t ₀  entre los satélites A y B. Describimos una solución basada en alcance dual unidireccional. 

En la época  t ₁  en el tiempo propio del satélite A, el satélite A realiza con el satélite B una medición de pseudodistancia ρ _AB  ( t ₁ ). Durante el siguiente subintervalo, el satélite B mide el pseudorango ρ _BA  ( t ₂ ) con el satélite A en el momento  t ₂  de su tiempo propio. Estas mediciones, que corresponden a diferentes épocas, son compartidas (cada satélite mide el rango hacia adelante ρ: AB y recibe el rango hacia atrás ρ: BA) y se puede escribir como:

Donde   se tienen en cuenta todos los efectos debidos a la relatividad, la polarización instrumental, el desplazamiento de la antena y ε _m  es el ruido de medición.

Para combinar las mediciones proporcionadas por los satélites A y B, es necesario calcular las correcciones dρ para devolverlas a la misma época común,  t ₀ , expresada en tiempo del sistema. En general, estas correcciones se pueden expresar nominalmente como: 

Donde   representa el pseudorango teórico calculado utilizando información orbital y de reloj anterior. La precisión de dicha corrección depende de la precisión del conocimiento a priori de los estados del receptor y del transmisor en las épocas del sistema  t ₀ ,  t ₁  y  t ₂ . Hay múltiples formas de recuperar los estados y relojes de los satélites en la época común  t ₀ : propagación dinámica si se dispone de vectores de estado tanto del receptor como del transmisor, modelos analíticos y aproximaciones lineales. 

Una aproximación lineal es válida siempre que la diferencia de tiempo  t ₂ – t ₁  sea lo suficientemente pequeña como para mantenerse bajo los supuestos de la aproximación lineal. Las correcciones lineales son función de la velocidad de los satélites y de la deriva de los relojes. Cada corrección se calcula:

con   y  . La velocidad   y   se toman respectivamente en los tiempos  t ₁  y  t ₁ –τ _AB .

El vector unitario de la línea de visión se calcula en el momento  t ₁  de la medición:

Utilizando el enlace por satélite en el otro sentido es fácil calcular la corrección  d ρ _BA

con 

La precisión de esta corrección está directamente relacionada con el intervalo de tiempo entre las dos mediciones de pseudodistancia  t ₂ – t ₁ , la precisión de la velocidad del satélite y la deriva del reloj (que se deducen del filtro de navegación global). Una vez calculadas las correcciones, podemos construir la medición bidireccional en la época común sumando las correcciones  d ρ:

Esto lleva a la siguiente formulación:

Las ecuaciones 19 y 20  tratan con la misma distancia geométrica en la época común y los mismos sesgos de reloj. Esto permite separar el reloj de los problemas de órbita calculando un alcance dual unidireccional:

En estas fórmulas, se puede suponer que los retrasos instrumentales incluidos en los términos γ ₁ , γ ₂  son suficientemente estables, por lo que no se producen cambios significativos entre  t ₀ ,  t ₁  y  t ₂ . Todos los retrasos de la relatividad (que tienen en cuenta las correcciones relativistas del reloj tanto en el receptor como en el transmisor y el efecto Shapiro) también pueden considerarse invariantes a lo largo de los pasos de tiempo. Las medidas  P  y  H  se pueden utilizar entonces en dos filtros independientes: un filtro para la determinación de la órbita y otro filtro para la sincronización del reloj. 

El alcance dual unidireccional corresponde al estado de la técnica, pero para aprovechar realmente esta solución, el protocolo de comunicación utilizado para el ISL debe respetar dos limitaciones principales:

• En un esquema de comunicación semidúplex, se debe incluir un subintervalo adicional al final de cada intervalo de tiempo determinado, durante el cual se comparte el alcance directo. Esto significa que A habla con B, luego B habla con A, y luego nuevamente A habla con B.  De esta manera, es posible que cualquier satélite recopile observaciones de alcance tanto hacia adelante como hacia atrás, necesarias para construir  P  ​​y  H.

• Si se explotan aproximaciones lineales, las duraciones de los subintervalos deben ser lo más cortas posible. La precisión de la corrección lineal dρ aplicada para llevar los observables a una época común depende directamente del tiempo transcurrido entre el avance y el retroceso  t ₂  –  t ₁ . Si este tiempo es demasiado largo (incluso mayor que unos pocos segundos), la aproximación lineal utilizada para calcular  d ρ ya no es válida y se introducen errores adicionales en las observaciones.

ODTS con mediciones ISL y GNSS terrestres

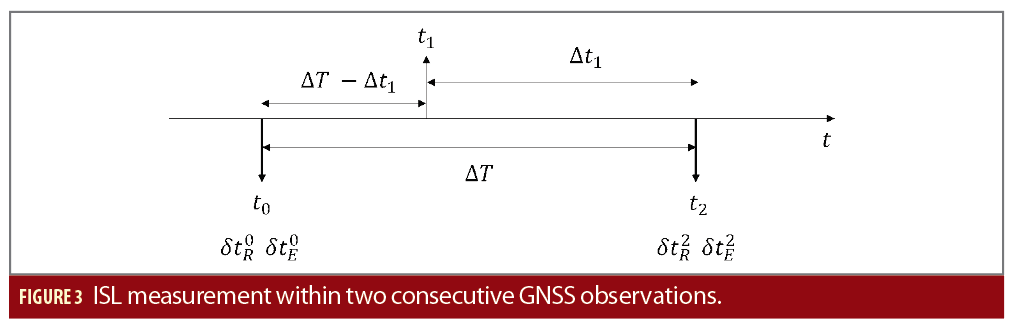
El principal desafío de las mediciones ISL es insertarlas en la medición GNSS terrestre global porque no son sincrónicas. Por lo general, las estaciones GNSS terrestres procesan las mediciones de distancia a una frecuencia determinada (dada por el paso del filtro), mientras que las mediciones ISL se registran en cualquier momento entre dos pasos consecutivos, de acuerdo con el plan de contacto específico y la definición ISL. Por lo tanto, no se pueden introducir sesgos de reloj provenientes de mediciones ISL; están en el filtro ODTS porque no representan el sesgo de sincronización del reloj en la misma época.

Suponiendo que el satélite R ha medido en la época  t ₁  el pseudorango cruzado ρ _RE  ( t ₁ ) con el satélite E, que se puede calcular mediante  la Ecuación 1,  se deben agregar dos sesgos de reloj adicionales al vector de estado para cada medición ISR. Entonces, una ecuación añade dos incógnitas al problema. Para reducirlos, los sesgos de reloj δt _R  ( t _r ) y δt _E  (t _e ) deben calcularse utilizando las resoluciones de instantáneas más cercanas. Suponiendo que la dinámica temporal del reloj del satélite evoluciona linealmente en intervalos cortos (unos pocos minutos), la desviación del reloj del satélite en el momento  t ₁  se puede expresar como la desviación del reloj del satélite en las épocas del sistema  t ₀  y  t ₂ . Un método clásico consiste en aplicar una interpolación lineal para calcular la información de compensación del reloj en el momento  t ₁  utilizando la información de compensación del reloj en los tiempos  t ₀  y  t ₂ , como se muestra en  la Figura 3.

Más precisamente, dado   y   en las épocas del sistema  t ₀  y  t ₂  correspondientes a dos pasos de filtro consecutivos ( t ₂ – t ₀ =∆ T ), podemos expresar   como (el mismo procedimiento se aplica al Satélite E):

Donde  f(t)  depende del método de interpolación específico seleccionado (esto se puede ampliar para incluir más puntos de interpolación). En la práctica, los intervalos de interpolación son muy pequeños porque el paso del filtro ODTS ∆ T  generalmente se fija entre 30 y 180 segundos para eliminar las correlaciones de tiempo entre mediciones.

Actuación

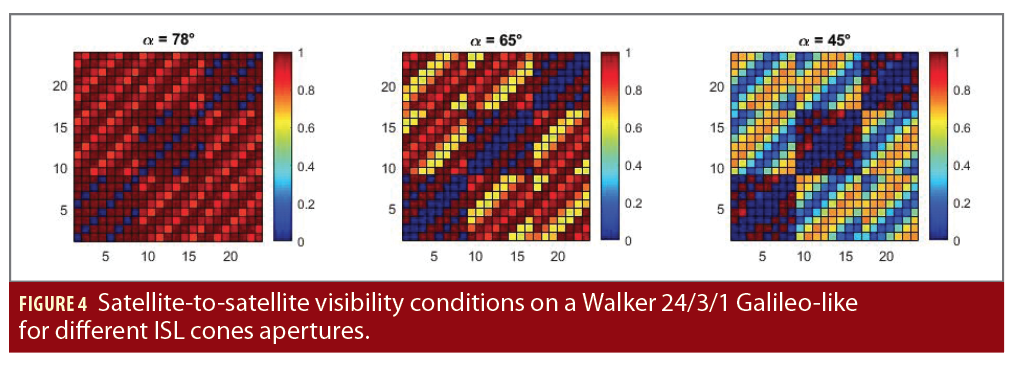
La evaluación del desempeño se realiza en un escenario sintético que introduce mediciones de ISL. Para ODTS terrestres se considera una red de 14 estaciones terrestres. La constelación de referencia es una Walker 24/3/1 con un semieje mayor igual a 29.600 km (constelación similar a Galileo, 24 satélites distribuidos uniformemente en tres planos orbitales con un espaciado RAAN de 120°). Las matrices muestran las condiciones de visibilidad de satélite a satélite durante un período de dos días. El ángulo de elevación mínimo dentro del marco de referencia ISL varía entre 12° (α=78° es la semiapertura del cono de visibilidad) y 45° (α=45°). El ángulo de elevación mínimo en el marco de referencia ISL se fijó en 12 °, correspondiente al primer gráfico a la izquierda de la  Figura 4  ([7] propone el mismo tipo de matriz de visibilidad para diferentes geometrías). 

El mapa en color muestra cuánto tiempo algunos satélites determinados están en visibilidad unos de otros. Los satélites en el mismo plano siempre están visibles entre sí, excluyendo un satélite eclipsado por la Tierra en el lado opuesto del plano orbital. Los satélites en diferentes planos tienen muy buenas condiciones de visibilidad >80% del tiempo. 

Mediciones terrestres y determinación de distancia entre satélites 

El alcance unidireccional terrestre se procesa con el alcance unidireccional ISL en el filtro ODTS. El primer gráfico de  la Figura 4  muestra que con α=78°, todos los satélites en otros planos tienen visibilidad >80% del tiempo, mientras que los satélites en el mismo plano (excluidos los satélites con un espaciado de anomalía real de 180°) están en visibilidad constante. . 

En este escenario simulado, el reloj del satélite se modela como un reloj Maser Pasivo de Hidrógeno (PHM). El error de medición que se puede alcanzar depende de la DLL y de las propiedades de la señal de alcance:

• Esquema de modulación de la señal de alcance.

• Espaciado temprano-tardío (para realizar la alineación entre la réplica y la señal recibida)

• Relación potencia de señal a ruido C/N ₀

• Tiempo previo a la integración

Los rendimientos esperados y simulados de las mediciones basadas en ISL son: 

• RMS < 0,05 m para error de observación del código de alcance unidireccional de satélite a satélite (1 sigma) para cualquier enlace establecido 

• RMS < 0,00095 m/s para error de observación Doppler unidireccional de satélite a satélite (1 sigma) para cualquier enlace establecido 

El filtro ODTS procesa observables de Código y Doppler. 

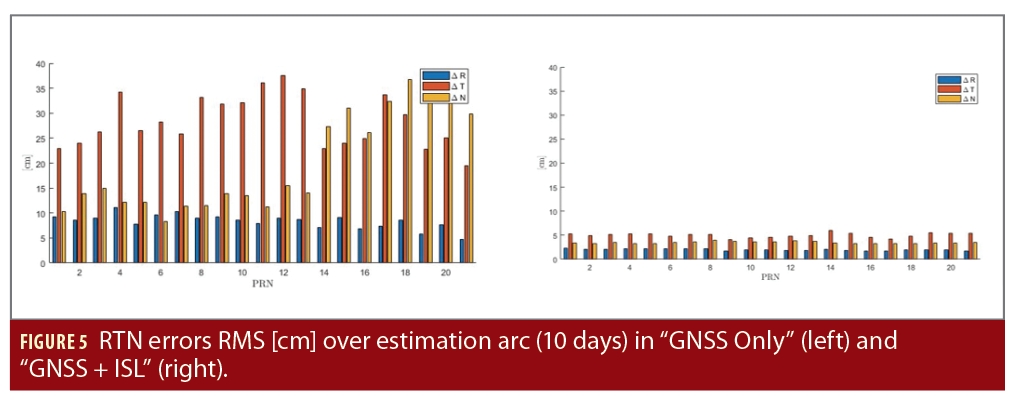
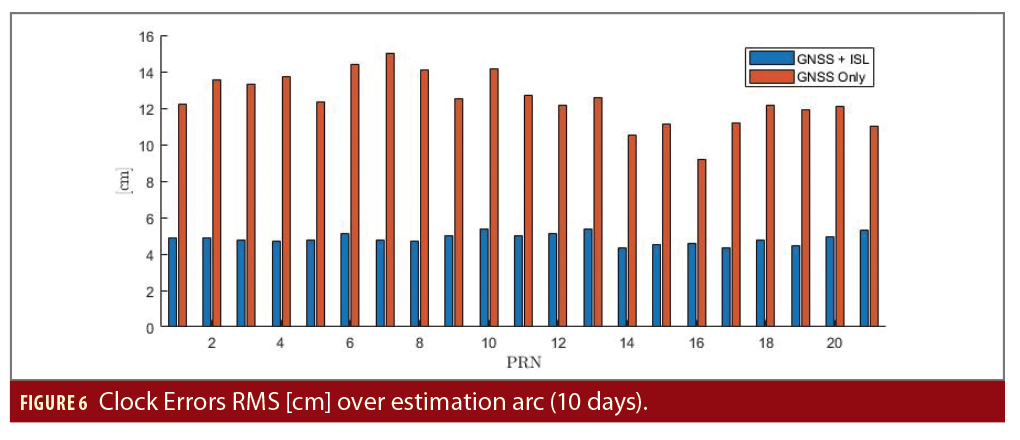
Evaluamos el rendimiento de dos maneras: comparando la órbita y el reloj estimados con los datos de referencia, la órbita y los relojes reales, y la mejora en el SISE del mensaje de navegación transmitido a los 20 y 100 minutos, respectivamente. Los errores de estimación se proyectan en el Marco Orbital Local (x, o radial, está alineado con el vector de posición del satélite; z, o normal, es paralelo al momento angular orbital e y, la dirección tangencial, completa la tríada). En este marco de referencia específico, es más fácil evaluar la mejora de la geometría del problema debido a los observables ISL y su impacto sobre los errores en la línea de visión usuario-satélite.  Las Figuras 5 y 6 muestran los errores durante la estimación (después de la convergencia) en un escenario con y sin observables ISL. Los errores se calculan durante 10 días en todos los satélites. Los valores RMS de la órbita se presentan en  la Figura 5.  Los errores de sincronización del reloj se muestran en  la Figura 6.

Las Figuras 5 y 6  muestran que los observables ISL mejoran drásticamente la observabilidad de todas las direcciones principales, tanto dentro como fuera del plano. Las líneas de visión ISL hacen que la geometría sea mucho más favorable. Los errores de reloj se reducen porque el filtro puede separar más fácilmente los errores orbitales a lo largo de la dirección radial de los errores de polarización del reloj. El RMS de los errores de posicionamiento 3D durante la estimación es inferior a 7 cm cuando se incluye el rango ISL y el Doppler dentro del filtro (con todas las hipótesis formuladas sobre el ruido ISL). 

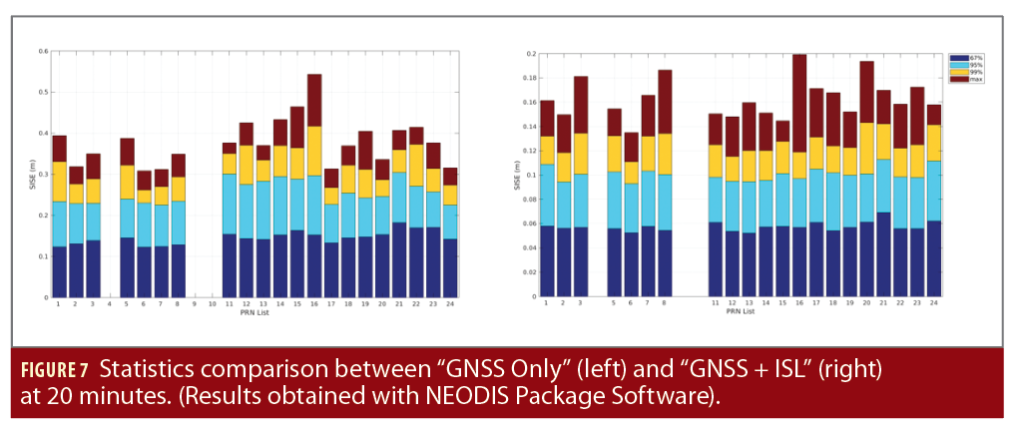
Los siguientes resultados se refieren a errores de mensajes de navegación con errores de propagación y compresión incluidos. Comprimir las efemérides en parámetros reducidos del mensaje de navegación introduce errores adicionales. El mensaje de navegación siempre se calcula sobre una efeméride propagada. El sesgo del reloj se extrapola utilizando el conocido polinomio de segundo orden. El percentil 95 de SISE para la peor ubicación del usuario (WUL) se evalúa para el peor satélite después de la convergencia de NEODIS (48 horas solo para GNSS y 24 horas para GNSS + ISL), utilizando los mensajes de navegación generados, a los 20 y 100 minutos, respectivamente.  (Tabla 1).  El WUL se define como un usuario ubicado en el borde de un cono de visibilidad de elevación de 5°. 

La Figura 7  compara los resultados de dos experimentos: mediciones GNSS únicamente y mediciones GNSS + mediciones ISL, ambos escenarios nominales, sin eventos temidos (se proporcionan detalles y estadísticas por satélite, los valores del 95% se muestran en azul claro).

ODTS a bordo con alcance entre satélites únicamente 

Siempre que se pierde el contacto con el suelo, la constelación GNSS puede continuar realizando su propio ODTS explotando únicamente observaciones ISL. Si asumimos que no se puede establecer ningún vínculo con el segmento terrestre, existen dos enfoques principales para un filtro de navegación autónomo a bordo que aproveche únicamente ISL: 

1. Distribuido:  Cada satélite realiza su propia ODTS utilizando el alcance hacia otros satélites, mensajes de navegación que contienen el último reloj recibido y estimaciones de órbita para todos los demás satélites y su covarianza asociada. 

2. Centralizado:  los rangos y los vectores de estado se comparten y centralizan en un filtro ODTS de constelación que estima los relojes y órbitas de todos los satélites al mismo tiempo.

El mensaje de navegación transmitido se calculará con respecto a una escala de tiempo común y permitirá a los usuarios calcular las posiciones de los satélites en un marco de referencia terrestre. Es por ello que se tendrán en cuenta dos cuestiones principales: cómo construir una escala de tiempo común y cómo extrapolar con precisión los parámetros de orientación de la Tierra y realizar la rotación desde el marco de referencia inercial al terrestre.

Sincronización horaria 

En ausencia de un reloj maestro común, el problema de la sincronización horaria no puede solucionarse imponiendo un único reloj físico de referencia. Por lo general, los relojes de los satélites se estiman con respecto a un reloj maestro elegido en tierra. 

Son posibles diferentes alternativas: 

1. Reloj maestro de satélite:  Un satélite determinado asume el papel de reloj maestro. Los sesgos del reloj se calculan con respecto a este SV específico. El rendimiento está limitado por la estabilidad del reloj y tiene el gran inconveniente de tener un único punto de fallo. 

2. Reloj compuesto:  se construye una escala de tiempo común utilizando todos o un subconjunto seleccionado de relojes SV. 

Se espera que una solución basada en un reloj compuesto proporcione una mejor estabilidad a largo plazo y también sea más robusta ante cualquier evento temido por satélite individual. Durante la navegación autónoma, no se puede lograr la sincronización con escalas de tiempo externas. Las limitaciones de la diferencia relativa entre la hora de referencia de la constelación y UTC no pueden controlarse directamente si no hay contacto con el suelo. 

Parámetros de orientación de la Tierra 

Cuando se pierde el contacto con el segmento terrestre y sólo se dispone de mediciones entre satélites, los parámetros de orientación de la Tierra se vuelven inobservables y el filtro no puede estimarlos. La consecuencia es menor con respecto a la dinámica de las constelaciones porque las órbitas se propagan en un marco inercial. Algunos modelos de fuerza dependen del marco fijo de la Tierra (debido al campo de gravedad), pero una mala orientación de unos pocos metros no cambia significativamente el campo de gravedad. El cálculo realizado a bordo sigue siendo muy preciso incluso en presencia de pequeños errores de orientación. La falta de actualización de los parámetros de orientación de la Tierra tiene un impacto crítico en la generación de mensajes de navegación porque está estrechamente ligado al marco fijo de la Tierra. Por tanto, es obligatorio que la constelación cuente con un modelo de predicción a bordo que pueda aplicarse hasta que se recupere el contacto con el suelo. Se pueden calcular modelos precisos a largo plazo a partir de datos históricos. Este modelo se puede cargar fácilmente en el segmento espacial durante operaciones nominales y usarse cuando se activa el modo autónomo. 

Conclusiones 

Las simulaciones que incluyen mediciones ISL dentro del paquete de software NEODIS demuestran que los observables basados ​​en ISL tienen un impacto significativo en el desempeño de la órbita y la estimación del reloj del satélite y, por lo tanto, en el desempeño del posicionamiento del usuario a través del mensaje de navegación. En el ODTS terrestre, hemos demostrado que los observables basados ​​en ISL permiten mejorar hasta tres veces la órbita SISE y el reloj con respecto a un ODTS basado únicamente en observaciones terrestres, logrando una órbita SISE de 11 cm al 95% y un reloj de 20 minutos. Esta tecnología podría hacer posible la navegación autónoma a bordo durante una pérdida prolongada de contacto entre la constelación y las estaciones terrestres. 

Referencias 

(1)  Fernández, FA (2011), “Inter-Satellite Ranging and Inter-Satellite Communication Links for Improvement GNSS Satellite Broadcast Navigation Data”, Advances in Space Research Volumen 47, Número 5, 1 de marzo de 2011, páginas 786-801 

(2)  Lv, Y. et al. (2020), “Evaluación de las estrategias de determinación de la órbita BDS-3 mediante seguimiento terrestre y observación de enlaces entre satélites”, Teledetección, 2020, 12

(3)  Wolf, R. (2000), “Determinación de la órbita y las efemérides de los satélites mediante enlaces entre satélites”, Disertación, 2000

(4)  Eissfeller, B. et al. (2000), “Determinación autónoma del estado de los satélites mediante el uso de enlaces bidireccionales”, Revista Internacional de Comunicaciones por Satélite 18 (2000): 325-346

(5)  Reglamento de Radiocomunicaciones de la UIT, Sección IV. Estaciones y sistemas de radio – Artículo 1.22, definición: servicio entre satélites / servicio de radiocomunicaciones entre satélites

(6)  https://www.esa.int/Enabling_Support/Space_Engineering_Technology/Shaping_the_Future/Optical_inter-satellite_links_are_best_tech_for_Galileo

(7)  Kur, T. et al. (2021).F “La aplicación de esquemas de conectividad de enlaces entre satélites en varios sistemas de navegación por satélite para la determinación de las correcciones de órbita y reloj: estudio de simulación”, Acta Geodaetica et Geophysica volumen 56, páginas 1–28 (2021)

(8)  Yang, Y. et al. (2019). “Determinación de la órbita mejorada del enlace entre satélites para BeiDou-3”, 2019 Journal of Navigation 73: 1-16

Autores

Marco Laurenti  es ingeniero de navegación en Thales Alenia Space. Tiene una maestría en Ingeniería Espacial y Astronáutica de la Universidad La Sapienza de Roma, Italia y una maestría avanzada en Ingeniería de Sistemas Espaciales del Institut Supérieur de l’Aéronautique et de l’Espace en Toulouse, Francia. Desde 2019, sus áreas de actividad son los algoritmos de determinación de órbita precisa LEO y determinación de órbita GNSS y sincronización horaria. 

Luc Maisonobe  es un experto en astrodinámica con más de 35 años de experiencia en todos los campos espaciales, desde los estudios hasta el análisis y las operaciones de misiones, y desde la observación de la Tierra hasta la navegación y las telecomunicaciones. Es el creador y desarrollador principal de la biblioteca de dinámica de vuelos espaciales de código abierto Orekit. Desde 2022 pertenece al equipo de orbitografía del Dominio de Navegación de Thales Alenia Space.

Pedro José Roldán Gómez  es especialista en sistemas de tiempo y frecuencia en Thales Alenia Space. Tiene un Doctorado en Climatología y dos maestrías en Ingeniería Aeroespacial y en Meteorología y Geofísica de la Universidad de Madrid, España. Sus áreas de actividad incluyen determinación de órbita GNSS y algoritmos de sincronización horaria, aplicaciones de GNSS para posicionamiento y temporización precisos, y algoritmos para transferencia de tiempo, generación y dirección de escalas de tiempo.

Julie Anton  es especialista en algoritmos de orbitografía en Thales Alenia Space. Tiene una maestría en Ingeniería Espacial y Aeronáutica del ISAE-Supaéro. Sus áreas de actividad incluyen la determinación precisa de la órbita LEO, la determinación de la órbita GNSS y los algoritmos de sincronización horaria y el análisis del rendimiento del sistema Galileo.

Pierre Guerin  es experto en algoritmos de orbitografía en Thales Alenia Space. Tiene una maestría en Astrofísica y Tecnología Espacial de la Universidad Paul Sabatier de Toulouse, Francia. Desde 2014, ha contribuido a varios sistemas de dinámica de vuelos espaciales, siendo su campo principal la determinación precisa de la órbita LEO y los algoritmos de determinación de la órbita y sincronización del tiempo GNSS.

Sébastien Trilles  es experto en orbitografía y algoritmos de integridad en Thales Alenia Space en Toulouse, Francia. Tiene un doctorado. en Matemática Pura de la Universidad Paul Sabatier y una maestría avanzada en Tecnología Espacial de ISAE-Supaero. Dirige el Departamento de Rendimiento y Procesamiento, donde se diseñan algoritmos de alta precisión que incluyen determinación de órbita, sincronización de reloj, transferencia de tiempo, generación de tiempo de referencia, integridad y algoritmos de modelado de ionosfera para sistemas GNSS y aumentación.